Signal Blocks¶
Signal Blocks include fucntions for processing and filter signals, control inputs and outputs, etc.
Signal Blocks
3D Table Interpolation
Returns the value obtained by interpolating the configured table with the input variables. First input represents rows, second input represents columns.
If out of range, the value for the closest limit will be taken.
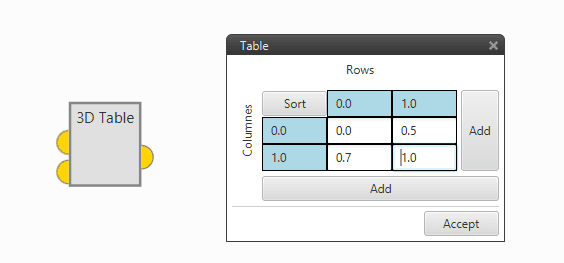
Table Interpolation
Note
IIR Block will return an error if the row or column values are not sorted from lowest to highest. In order to solve this, just click on the Sort button.
Bound
Returns the input in. If the input is out of range, the limit is returned instead. If limits are not defined, they are asumed to be infinity.
In range will be true if the input is within the limits and false if it is not.

Bound Block
Tip
Use the Bound block to monitor that critical parameters inside your system are within operational limits (i.e. voltage levels). If not OK, in range can be used to activate an alarm.
IIR Filter
Rate Limiter
Returns the Current input signal, but limiting its maximum rate of change.
The limits are defined in Input units/s.
If the rate of change of the input is higher than the maximum, the output will try to converge to the input, but respecting the imposed maximum rate of change.
The first time the block is executed the output will be equal to Init.

Rate limiter Block
Tip
The Rate limiter block can be used to avoid steps and instant spikes in the control signals, efectively reducing control noise and smoothing the flight.
Ramp
