Math blocks¶
Math blocks allow to perform a wide variety of mathematical operations.
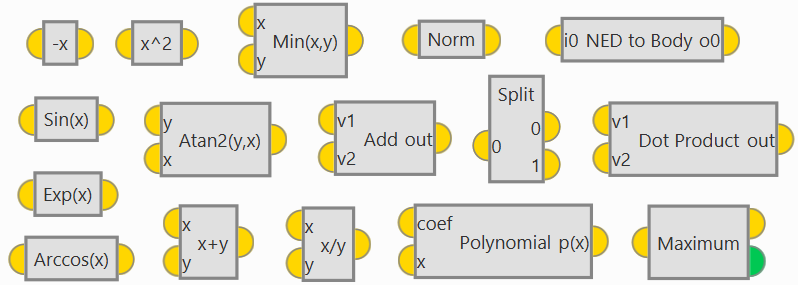
Math blocks¶
f(x)¶
Math blocks with 1 input and 1 output.
All f(x) math blocks have the same input and output:
Input
: Input value, real variable or constant.Output
: Output value.
Warning
All these blocks express the output value in radians.
Users will find the following blocks:
-x: Change of sign.
1/x: Inverse of the input (1/x).
[-0.5,0.5] Wrap: Wrapping to the range [-0.5, 0.5].
[-pi,pi] Unwrap: Angle unwrap from [-pi, pi] limits. This block converts an angle signal in the range [-pi, pi] to a continuous signal in the range [-inf, +inf] assuming the smallest angle change between execution steps.
[-pi,pi] Wrap: Angle wrapping to the range [-pi, pi] radians.
[0,1] Wrap: Wrapping to the range [0, 1].
[0,2pi] Wrap: Angle wrapping to the range [0, 2*pi] radians.
Arccos(x): Arccos function.
Arcsin(x): Arcsin function.
Arctan(x): Arctangent function.
Ceil(x): Closest intger rounding towards plus infinity.
Cos(x): Cosine function.
Exp(x): Natural exponent (e number to the power of the input of the block).
Floor(x): Closest integer rounding towards minus infinity.
Log(x): Natural logarithm.
Round(x): Rounding to closest integer.
Sign(x): Sign of the input. It returns ‘1’ if the input is positive or zero and ‘-1’ if negative.
Sin(x): Sine function.
Sqrt(x): Square root.
Tan(x): Tangent function.
x^2: Square of the input.
|x|: Absolute value.
f(x,y)¶
Math blocks with 2 inputs and 1 output.
All f(x,y) math blocks have the same inputs and output:
Inputs
: Input value, real variable or constant. : Input value, real variable or constant.Output
: Output value.
Users will find the following blocks:
Atan2(y,x): Calculates one unique arc tangent value, where the signs of both arguments are used to determine the quadrant of the result.
Max(x,y): Returns the maximum value of the two inputs.
Min(x,y): Returns the minimum value of the two inputs.
Remainder(x/y): Remainder block computes the remainder of the division with the first input as numerator and second input as denominator.
x*y: Mulitplier block.
x+y: Adder block.
x-y: Subtract block computes the subtraction of the first input minuts the second input.
x/y: Divider block computes the division with the first input as numerator and second input as denominator.
x^y: Computes the first input raised to the power of the second input.
Polynomial¶
This block performs a polynomial evaluation, it returns the value of the polynomial defined by the coefficients for the value of x.
Polynomial block¶
Inputs
coef: Array of polynomial coefficients. The order is in increasing order of powers, that is first element is the independent term, second term is the proportional term, third the quadratic term, etc. x: Value of evaluation of the polynomial.Output
p(x): Result of the polynomial evaluation.
Vectors¶
These are blocks that perform operations with vectors.
Add: Adds two vectors together.
Add Elements: Adds all the element of the input vector.
azeld -> xyz: Conversion from azimuth, elevation and distance to NED (North, East, Down).
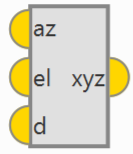
azeld -> xyz block¶
Inputs
az: Azimuth in radians. el: Elevation in radians. d: Distance in meters.Output
xyz: NED (North, East, Down) vector in meters.
Body to NED: Rotates a vector from the Body frame of reference to North, East, Down.
Body to NED block¶
Input
i0: Vector in Body frame.Output
o0: Vector in NED frame.
Bundle: Returns a vector whose components are the inputs of the block. In its configuration, the user can set the number of inputs.
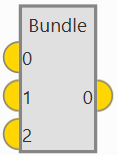
Bundle block¶
Cross product: Produces the cross product multiplication of the input vectors.
Dot Product: Returns the dot product of the input vectors.
Linear Transformation: Returns the input vector multiplied by the transformation matrix. In order to edit the transformation matrix, double click on the block.
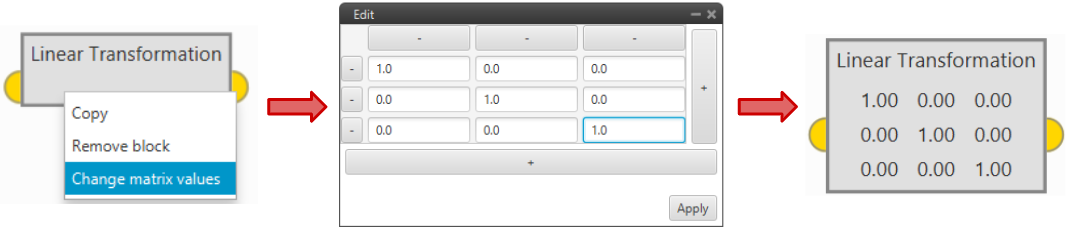
Linear Transformation block¶
m x v: Multiplies a 3x3 matrix by a vector of size 3.
Inputs
m: Matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.
That is, the input vector must be: [00 10 20 01 11 21 02 12 22] Where the matrix will be: \(\begin{pmatrix} 00 & 01 & 02 \\ 10 & 11 & 12 \\ 20 & 21 & 22 \end{pmatrix}\) v: Column vector with 3 elements.Output
Pin 0: Product of the matrix and the vector, with 3 elements.
m1 x m2: Multiplies two 3 by 3 matrices.
Inputs
m1: First matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on. m2: Second matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.Output
Pin 0: Matrix product of both matrices, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.
m1 x m2T: Multiplies a 3x3 matrix by the transpose of another 3x3 matrix.
Inputs
m1: First matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on. m2: Second matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.Output
Pin 0: Matrix product of the two inputs, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.
m1T x m2: Multiplies the transpose of a 3x3 matrix by another 3x3 matrix.
Inputs
m1: First matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on. m2: Second matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.Output
Pin 0: Product of both matrices, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.
m1T x m2T: Multiplies the transpose of two 3x3 matrices.
Inputs
m1: First matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on. m2: Second matrix, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.Output
Pin 0: Matrix product of both matrices, as an array of 9 elements, where the element 0 is 00 of the matrix, the 1 is 10 and so on.
Mat2quat: Transforms a 3-by-3 rotation matrix (
input) into its equivalent quaternion ( output).In its configuration users can select whether to conjugate the quaternion or not.
Max: Returns the value and position (
integer output) of the highest component of the input vector.Min: Returns the value and position (
integer output) of the lowest component of the input vector.Multiply Elements: Returns the product of the components of the input vector.
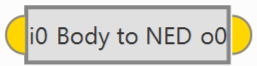
NED to Body: Rotates a vector from the North, East, Down frame of reference to Body.
NED to Body block¶
Input
i0: Vector in Body frame.Output
o0: Vector in NED frame.
Norm: Computes the norm of the input vector.
Quat2mat: Transforms a quaternion (
input) into its equivalent 3-by-3 rotation matrix ( output).In its configuration users can select whether to transpose the matrix or not.
Scale: Multiply the input vector (vIN) by a scalar value (k).
Split Bool: This block takes a boolean vector as input and splits it into as many outputs as the user wishes, each one of them can be a vector or a single value from the input.
Each output produces a vector with the size (number of elements) indicated in Size from the element of the input vector indicated in the Index parameter.
In the following example:
The first output produces a vector of size 4 with the first four elements (from 0 to 3).
The second output only generates a vector of size 1 with the fifth element (4).
The third output produces a vector of size 3 with the third to fifth elements (from 2 to 4).
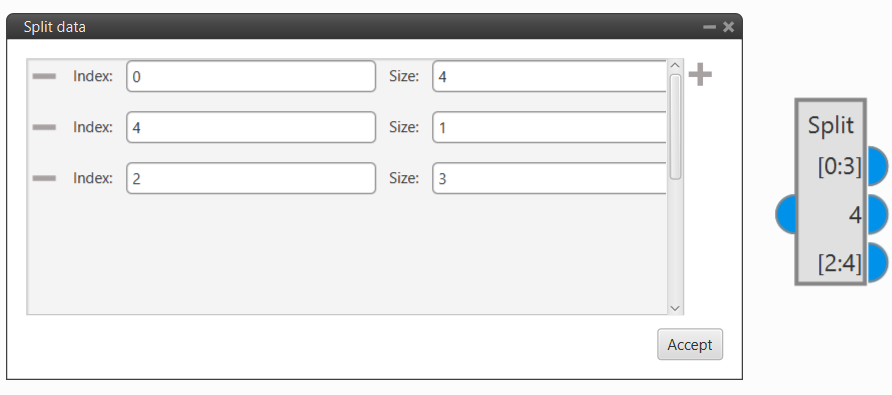
Split Bool block example¶
Split Real: This block works in the same way as Split Bool block does. Nonetheless, Split Real operates with real instead of boolean variables.
Substract: Subtracts from the first input vector (v1) the other input vector (v2).
Vector rotation: Rotates a given vector of 3 elements (
vector to rotate) by the provided rotation angles ( rotation angles).xyz -> azeld: Conversion from NED (North, East, Down) to azimuth, elevation and distance.
xyz -> azeld block¶
Input
xyz: NED (North, East, Down) vector in meters.Outputs
az: Azimuth in radians. el: Elevation in radians. d: Distance in meters.