Advanced Cooling Circuit Design

The power electronics of the MC110 will produce heat and its temperature will increase. To prevent overheating, the heat will be absorbed by a liquid coolant according to the following equation:

\(Q=m \cdot c \cdot (T_{out} - T_{in})\)

• \(Q\): heat produced by one single MC110.

• \(m\): coolant mass flow.

• \(c\): coolant specific heat.

• \(T_{out}\): temperature of the coolant at the output of the coldplate and at the input of the radiator.

• \(T_{in}\): temperature of the coolant at the input of the coldplate.

\(Q\) is assumed to be completely absorbed by the coolant, this assumption is considering the worst case scenario (adiabatic environment, which does not help at all).

The value of \(Q\) depends strongly on the switching frequency, input voltage (from battery) and motor power (hence intensity consumption). It can be obtained from the following tables, which assume an input coolant of water at 30 ºC (\(T_{in}\)) and 6 l/min:

Q for 10 kHz switching frequency (W)
Motor power (kW)	Battery voltage
	800 V	550 V	100 V
15	200	250	950
30	400	450	*
45	600	750	*
60	850	1000	*
75	1100	1350	*
95	1350	1700	*
110	1750	2200	*

Q for 16 kHz switching frequency (W)
Motor power (kW)	Battery voltage
	800 V	550 V	100 V
15	300	300	1000
30	550	600	*
45	850	950	*
60	1150	1300	*
75	1500	1750	*
95	2050	2250	*
110	2550	3000	*

Q for 22 kHz switching frequency (W)
Motor power (kW)	Battery voltage
	800 V	550 V	100 V
15	350	350	1050
30	700	750	*
45	1100	1200	*
60	1550	1650	*
75	2050	2250	*
95	2650	*	*
110	*	*	*

Warning

*: These situations involve an intensity higher to 250 A or overheating.

Once the heat transfer has been defined, the radiator can be chosen according to the required heat transfer capacity. Considering that each radiator dissipates the heat of several motor controllers.

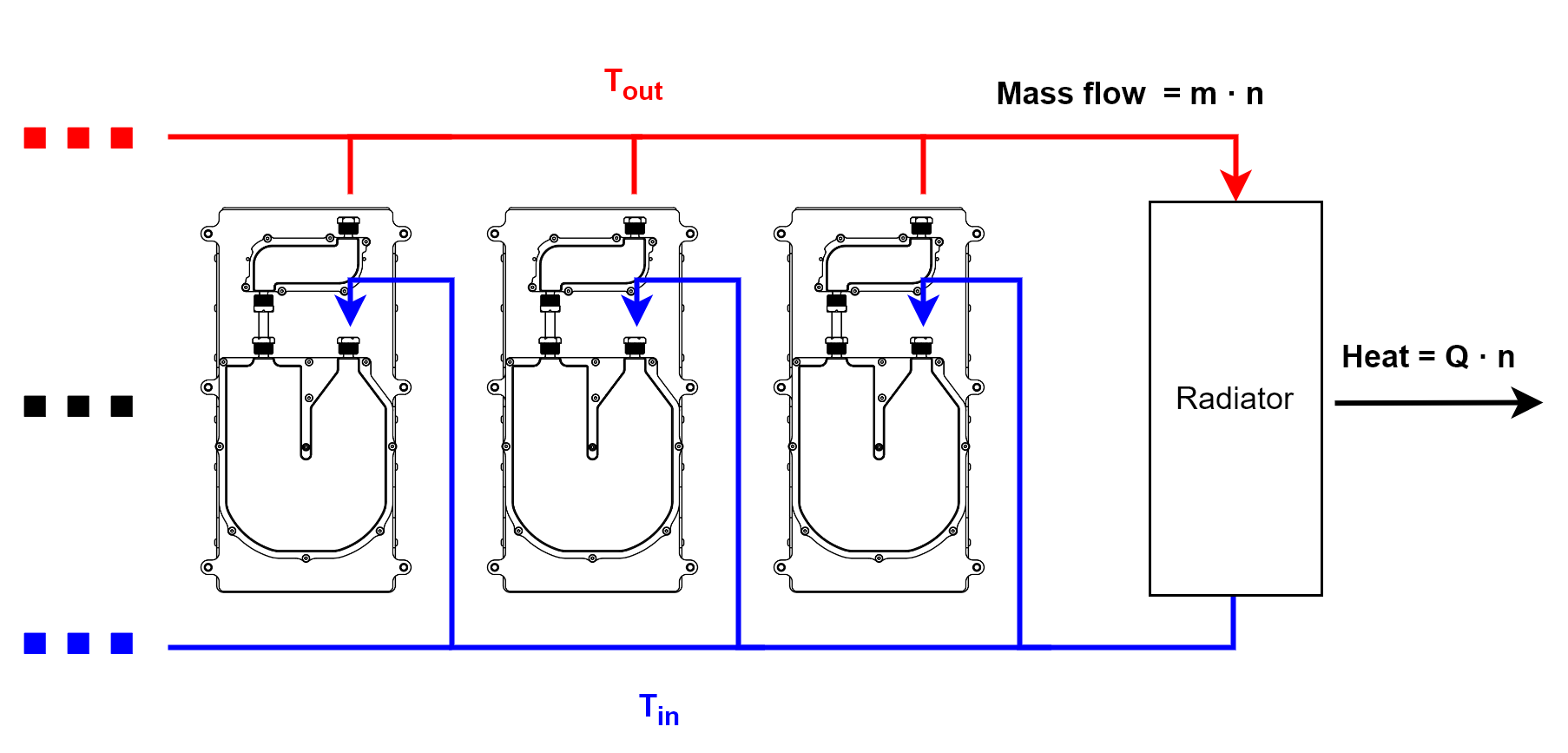
Simplified diagram for multiple controllers

\(H = Q \cdot n/(T_{out} - T_{amb})\)

• \(H\): heat transfer capacity.

• \(n\): number of motor controllers for the radiator.

• \(T_{amb}\): ambient temperature.

\(H = \frac{Q \cdot n}{T_{in} + Q/(m \cdot c) - T_{amb}}\)

Applying the previous equation to one MC110 obtains the tables of the Simplified Cooling Circuit Design.